# Knowledgedump.org - Maximum non-overlapping segment problem.
# This python script imports a batch of segment images and finds the combination of segments that covers
# the largest possible area, without any of the segments overlapping.

# Required packages: numpy, pulp, pillow

# For this script, the images are assumed to be placed in a "random_segments" folder, within the same directory as the script.
# The individual image files are named "segment_i.png", with i = 1, ..., 1000.

# NOTE: On most machines we have to restrict the number of segments for our problem, since the problem is too large for the
#       default pulp solver (cbc). This could be solved by:
#       - improving the ILP problem formulation, by adding/replacing constraints, e.g. checking for multiple overlapping segments,
#         for a tighter LP relaxation (instead of x_1+x_2 <= 1, x_2+x_3 <= 1, x_1+x_3 <= 1, use x_1+x_2+x_3 <= 1)
#       - using a commercial solver (Gurobi, CPLEX)
#       - getting more RAM
# We simply limit the number of images for our problem here and reduce the problem to a managable size.

import numpy as np
import pulp
from PIL import Image
import os


# General idea:
# First, we will import all .png files and convert the black&white image segments into binary matrices,
# with 0/false for black and 1/true for white. Then, we assign a cost and a weight variable to each segment.
# The cost will be equal to the sum of pixels/array entries that are white/1 and the binary LpVariable will determine,
# whether this segment is selected for our maximum non-overlapping segment combination (0 if not picked, 1 otherwise).
# Our optimization goal will be to maximize the energy/cost of picked segments, which corresponds to the largest area covered.
# Since the segments need to be non-overlapping, we will need to add constraints, which enforce this.

if __name__ == "__main__":
    # Set number of images. As noted before: The maximum number your machine can handle may vary. If solver gets stuck,
    # reduce this number or apply one of the solutions above.
    img_num = 400

    # Import images, save as 0/1 arrays. Requires "random_segments" folder in this script's directory.
    seg_array = []
    current_dir = os.path.dirname(os.path.abspath(__file__))
    # Images are named segment_1.png, segment_2....
    for i in range(1, img_num+1):
        # Images are loaded with pillow and converted to grayscale.
        img = Image.open(os.path.join(current_dir, f"random_segments/segment_{i}.png")).convert("L")
        # PIL.Image objects can be directly transformed to numpy arrays. Since the images are black and white,
        # we use the data type bool, with black corresponding to false and white to true.
        seg_array.append(np.asarray(img, dtype=bool))

    # Calculate the cost vector theta for our optimization problem. This is simply the total sum of white pixels/true values
    # in each image/array.
    theta = [np.sum(seg_arr_i) for seg_arr_i in seg_array]

    # Set up ILP maximization problem, using pulp library.
    ilp = pulp.LpProblem("maximum_segmentation", pulp.LpMaximize)

    # Set up LpVariables seg_i, assigning binary weights to all segments (0 = don't pick segment, 1 = pick segment).
    # Note: The LpVariable indices are 1, ..., img_num, like for the file names. Thus, theta[i-1] corresponds to mu[i].
    mu = pulp.LpVariable.dicts("seg", range(1, img_num+1), lowBound=0, upBound=1, cat="Binary")

    # Set up ILP objective to maximize, theta * mu:
    ilp += pulp.lpSum([theta[i-1]*mu[i] for i in range(1, img_num+1)])

    # Define constraints - if two segments have overlap, set sum of their weights to <= 1
    # (i.e. only one of the segments can be selected).
    for i in range(1, img_num+1):
        j = i + 1
        while j < img_num+1:
            # To check for an overlap between segments i and j, we check if there is any index,
            # for which both arrays have the value "True" (corresponding to an overlap in a white pixel).
            if np.any(seg_array[i-1] & seg_array[j-1]):
                ilp += pulp.lpSum(mu[i] + mu[j]) <= 1
            j += 1

    # Now that the optimization problem is set up, we call the pulp ILP solver and print results.
    # Due to the larger size of the problem here, we enable multithreading, so that up to 8 cores are used.
    # It appears that the solver is rather bottlenecked by RAM than CPU power though.
    solver = pulp.getSolver("PULP_CBC_CMD", threads=8)
    ilp.solve(solver)

    # After the problem is solved:
    # Fetch indices of segments used, to achieve the maximum non-overlapping segment combination.
    indices_used = []
    for var in ilp.variables():
        if(var.value() == 1):
            #Get index from the number after the underscore of the variable name and convert to integer.
            indices_used.append(int(var.name.split("_")[-1]))

    # Print objective value of the optimization problem to console, corresponding to the number of
    # white pixels for the maximum non-overlapping segment combination, as well as the indices of the
    # segments used therein.
    print("Area covered with segments (in pixels): ", ilp.objective.value())
    print(f"Segments used: {sorted(indices_used)}")

    # Merge used arrays, to create an image of all (non-overlapping) segments with maximum area, by summing them.
    seg_img = sum([seg_array[i-1] for i in indices_used])

    # Create an image containing all selected (non-overlapping) segments.
    output_img = Image.fromarray(np.uint8(seg_img * 255))
    output_img.save(os.path.join(current_dir, f"Segmentation_Result_{img_num}.png"))

            
            
... and so on ...
        

            
Console output:
            

            
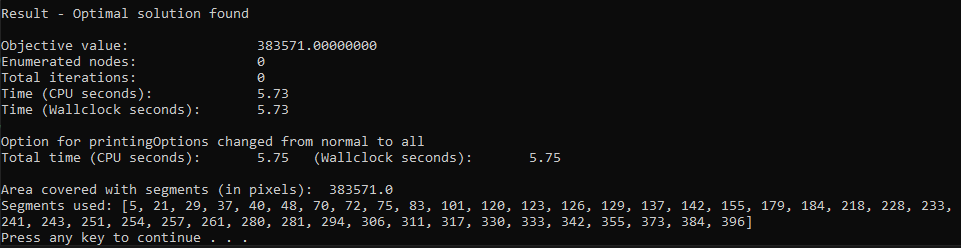
Image output: